Extenhancing understanding of the Pythagorean theorem
We well know the Pythagorean Theorem as “the sum of the areas of the squares on the legs of a right triangle is equal to the area of the square on the hypotenuse.” Visualization of the squares constructed on each side of the right triangle is an essential component in developing a robust concept image of “Pythagorean theorem.”
Once we have guided our students to connect the geometric representation with the algebraic representation of the relationship, we can further deepen their conceptual understanding, broaden their concept image, and promote reasoning and sense making through a series of tasks such as the following.
This is a particularly fruitful exploration using dynamic geometry software where figures can be resized and areas can be calculated within the program. But the constructions can also be done with compass and straightedge, allowing for a ruler to approximate measures of dimensions and a protractor for interior angles on the third task (unless you’re really motivated by the challenge of the compass/straightedge construction for a regular pentagon).
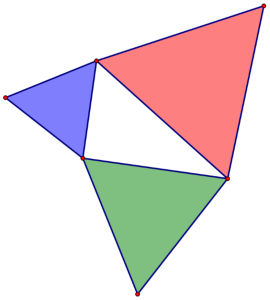
Task 1: Construct a right triangle. Construct an equilateral triangle on each side of the right triangle. Calculate the areas of the equilateral triangles. What do you observe? Make a conjecture.
Task 2: Construct a second right triangle. Construct a circle (or semicircle) on each side of the triangle such that the side corresponds to the diameter. Calculate the areas of the circles (or semicircles). What do you observe? Make a conjecture.
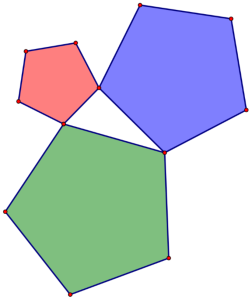
Task 3 (greater challenge): Construct a third right triangle. Draw a regular pentagon on each side of the triangle. You may want to determine the measure of an interior angle for an equilateral pentagon. Calculate the areas of the pentagons. What so you observe?
Task 4 (extension): What additional cases might you try exploring? (An isosceles triangle, a rectangle, an equilateral hexagon,…?) Are the outcomes similar or different?
Task 5 (summary): Make an overall conjecture regarding your findings.
Task 6 (reasoning & proof): Write a well-justified explanation of your findings or write an algebraic proof for several of your cases.
Task 7 (reflection): Were you surprised by the results of your explorations? What mathematical skills did you need to apply in this investigation? Describe several new mathematical understandings you now have.
Enhancing our knowledge from the research:
Concept image contrasted with concept definition. (Tall & Vinner, 1981)
“We shall use the term concept image to describe the total cognitive structure that is associated with the concept, which includes all the mental pictures and associated properties and processes. It is built up over the years through experiences of all kinds, changing as the individual meets new stimuli and matures….As the concept image develops it need not be coherent at all times.
We shall regard the concept definition to be a form of words used to specify that concept. It may be learnt by an individual in a rote fashion or more meaningfully learnt and related to a greater or lesser degree to the concept as a whole. It may also be a personal reconstruction by the student of a definition. Whether the concept definition is given to him or constructed by himself, he may vary it from time to time. In this way a personal concept definition can differ from a formal concept definition, the latter being a concept definition which is accepted by the mathematical community at large.”
Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational studies in mathematics, 12(2), 151-169. https://homepages.warwick.ac.uk/staff/David.Tall/pdfs/dot1981a-concept-image.pdf
Tall, D. (1988). Concept image and concept definition, Senior secondary mathematics education, (ed. Jan de Lange, Michiel Doorman), OW&OC Utrecht, 37– 41. https://homepages.warwick.ac.uk/staff/David.Tall/pdfs/dot1988e-concept-image-icme.pdf


Testing the comment feature.